
Bram Verhoef | Director of Customer Engineering & Success at AXELERA AI
Summary
Convolutional neural networks (CNNs) still dominate today’s computer vision. Recently, however, networks based on transformer blocks have also been applied to typical computer vision tasks such as object classification, detection, and segmentation, attaining state-of-the-art results on standard benchmark datasets.
However, these vision-transformers (ViTs) are usually pre-trained on extremely large datasets and may consist of billions of parameters, requiring teraflops of computing power. Furthermore, the self-attention mechanism inherent to classical transformers builds on quadratically complex computations.
To mitigate some of the problems posed by ViTs, a new type of network based solely on multilayer perceptrons (MLPs), has recently been proposed. These vision-MLPs (V-MLP) shrug off classical self-attention but still achieve global processing through their fully connected layers.
In this blog post, we review the V-MLP literature, compare V-MLPs to CNNs and ViTs, and attempt to extract the ingredients that really matter for efficient and accurate deep learning-based computer vision.
Introduction
In computer vision, CNNs have been the de facto standard networks for years. Early CNNs, like AlexNet [1] and VGGNet [2], consisted of a stack of convolutional layers, ultimately terminating in several large fully connected layers used for classification. Later, networks were made progressively more efficient by reducing the size of the classifying fully connected layers using global average pooling [3]. Furthermore these more efficient networks, among other adjustments, reduce the spatial size of convolutional kernels [4, 5], employ bottleneck layers and depthwise convolutions [5, 6], and use compound scaling of the depth, width and resolution of the network [7]. These architectural improvements, together with several improved training methods [8] and larger datasets have led to highly efficient and accurate CNNs for computer vision.
Despite their tremendous success, CNNs have their limitations. For example, their small kernels (e.g., 3×3) give rise to small receptive fields in the early layers of the network. This means that information processing in early convolutional layers is local and often insufficient to capture an object’s shape for classification, detection, segmentation, etc. This problem can be mitigated using deeper networks, increased strides, pooling layers, dilated convolutions, skip connections, etc., but these solutions either lose information or increase the computational cost. Another limitation of CNNs stems from the inductive bias induced by the weight sharing across the spatial dimensions of the input. Such weight sharing is modeled after early sensory cortices in the brain and (hence) is well adapted to efficiently capture natural image statistics. However, it also limits the model’s capacity and restricts the tasks to which CNNs can be applied.
Recently, there has been much research to solve the problems posed by CNNs by employing transformer blocks to encode and decode visual information. These so-called Vision Transformers (ViTs) are inspired by the success of transformer networks in Natural Language Processing (NLP) [9] and rely on global self-attention to encode global visual information in the early layers of the network. The original ViT was isotropic (it maintains an equal-resolution-and-size representation across layers), permutation invariant, based entirely on fully connected layers and relying on global self attention [10]. As such, the ViT solved the above-mentioned problems related to CNNs by providing larger (dynamic) receptive fields in a network with less inductive bias.
This is exciting research but it soon became clear that the ViT was hard to train, not competitive with CNNs when trained on relatively small datasets (e.g., IM-1K, [11]), and computationally complex as a result of the quadratic complexity of self-attention. Consequently, further studies sought to facilitate training. One approach was using network distillation [12]. Another was to insert CNNs at the early stages of the network [13]. Further attempts to improve ViTs re-introduced inductive biases found in CNNs (e.g., using local self attention [14] and hierarchical/pyramidal network structures [15]). There were also efforts to replace dot-product QKV-self-attention with alternatives [e.g. 16]. With these modifications now in place, vision transformers can compete with CNNs with respect to computational efficiency and accuracy, even when trained on relatively small datasets [see this blog post by Bert Moons for more discussion on ViTs].
Vision MLPs
Notwithstanding the success of recent vision transformers, several studies demonstrate that models building solely on multilayer perceptrons (MLPs) — so-called vision MLPs (V-MLPs) — can achieve surprisingly good results on typical computer vision tasks like object classification, detection and segmentation. These models aim for global spatial processing, but without the computationally complex self-attention. At the same time, these models are easy to scale (high model capacity) and seek to retain a model structure with low inductive bias, which makes them applicable to a wide range of tasks [17].
Like ViTs, the V-MLPs first decompose the images into non-overlapping patches, called tokens, which form the input into a V-MLP block. A typical V-MLP block consists of a spatial MLP (token mixer) and a channel MLP (channel mixer), interleaved by (layer) normalization and complemented with residual connections. This is illustrated in Figure 1.
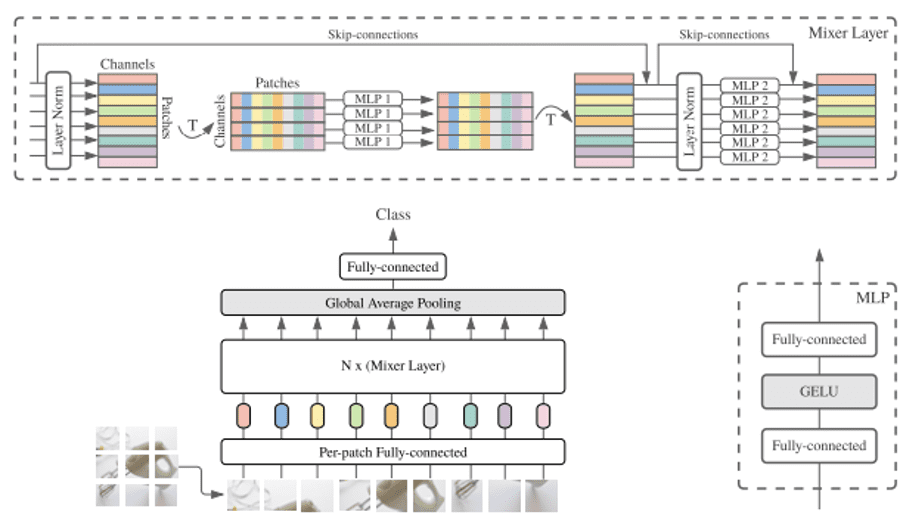
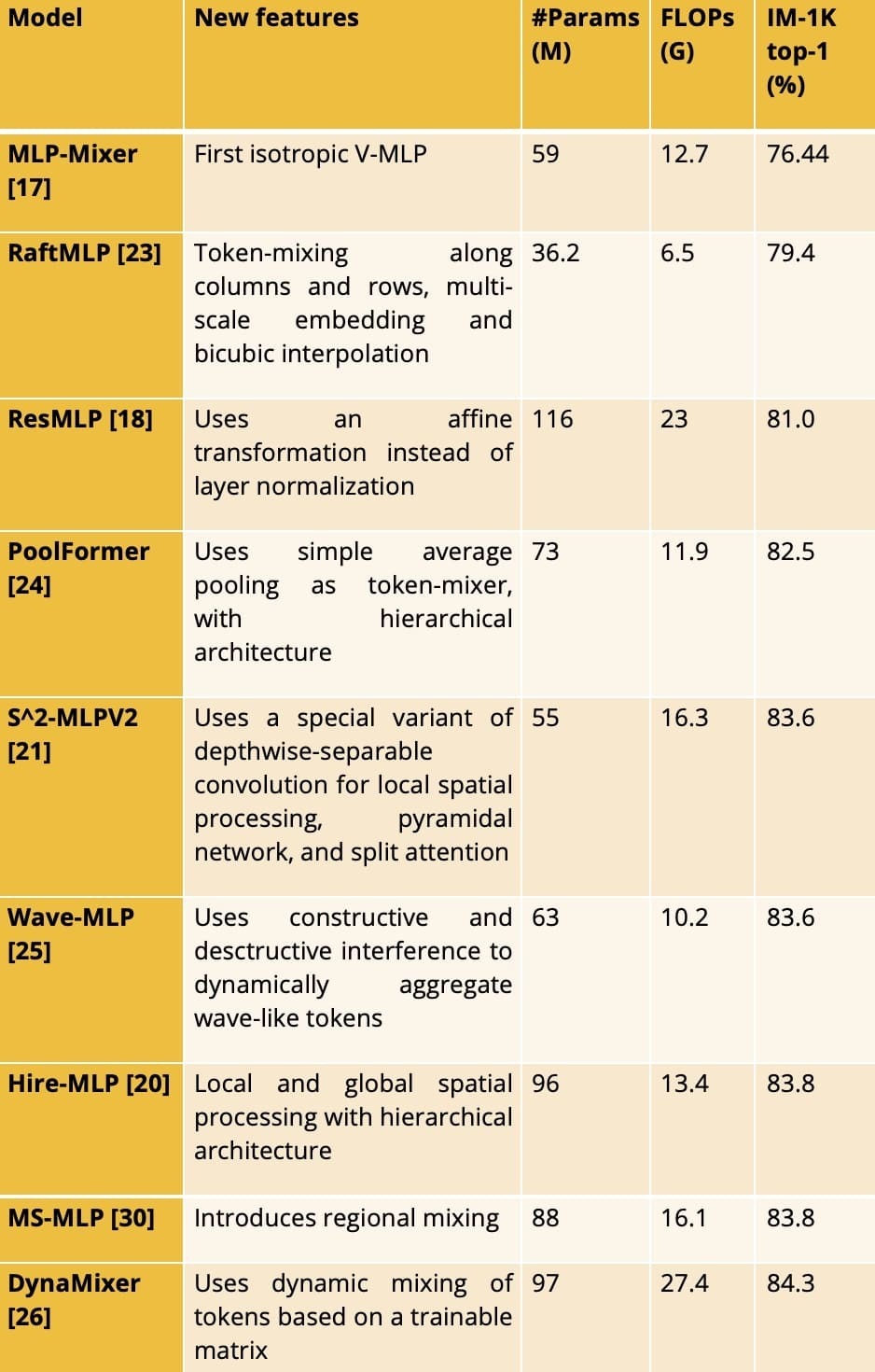
Table 1. Overview of some V-MLPs. For each V-MLP, we present the accuracy of the largest reported model that is trained on IM-1K only.
Here the spatial MLP captures the global correlations between tokens, while the channel MLP combines information across features. This can be formulated as follows:
Y=spatialMLP(LN(X))+X, Z=channelMLP(LN(Y))+Y,
Here X is a matrix containing the tokens, Y consists of intermediate features, LN denotes layer normalization, and Z is the output feature of the block. In these equations, spatialMLP and channelMLP can be any nonlinear function represented by some type of MLP with activation function (e.g. GeLU).
In practice, the channelMLP is often implemented by one or more 1×1 convolutions, and most of the innovation found in different studies lies in the structure of the spatialMLP submodule. And, here’s where history repeats itself. Where ViTs started as isotropic models with global spatial processing (e.g., ViT [10] or DeiT [12]), V-MLPs did so too (e.g., MLP-Mixer [17] or ResMLP [18]). Where recent ViTs improved their accuracy and performance on visual tasks by adhering to a hierarchical structure with local spatial processing (e.g., Swin-transformer [14] or NesT [19]), recent V-MLPs do so too (e.g., Hire-MLP [20] or S^2-MLPv2 [21]). These modifications made the models more computationally efficient (fewer parameters and FLOPs), easier to train and more accurate, especially when trained on relatively small datasets. Hence, over time both ViTs and V-MLPs re-introduced the inductive biases well known from CNNs.
Due to their fully connected nature, V-MLPs are not permutation invariant and thus do not necessitate the type of positional encoding frequently used in ViTs. However, one important drawback of pure V-MLPs is the fixed input resolution required for the spatialMLP submodule. This makes transfer to downstream tasks, such as object detection and segmentation, difficult. To mitigate this problem, some researchers have inserted convolutional layers or, similarly, bicubic interpolation layers, into the V-MLP (e.g., ConvMLP [22] or RaftMLP [23]). Of course, to some degree, this defies the purpose of V-MLPs. Other studies have attempted to solve this problem using MLPs only (e.g., [20, 21, 30]), but the data-shuffling needed to formulate the problem as an MLP results in an operation that is very similar or even equivalent to some form of (grouped) convolution.
See Table 1 for an overview of different V-MLPs. Note how some of the V-MLP models are very competitive with (or better than) state-of-the-art CNNs, e.g. ConvNeXt-B with 89M parameters, 45G FLOPs and 83.5% accuracy [28].
What matters?
It is important to note that the high-level structure of V-MLPs is not new. Depthwise-separable convolutions for example, as used in MobileNets [6], consist of a depthwise convolution (spatial mixer) and a pointwise 1×1 convolution (channel mixer). Furthermore, the standard transformer block comprises a self-attention layer (spatial mixer) and a pointwise MLP (channel mixer). This suggests that the good performance and accuracy obtained with these models results at least partly from the high-level structure of layers used inside V-MLPs and related models. Specifically, (1) the use of non-overlapping spatial patch embeddings as inputs, (2) some combination of independent spatial (with large enough spatial kernels) and channel processing, (3) some interleaved normalization, and (4) residual connections. Recently, such a block structure has been dubbed “Metaformer” ([24], Figure 2), referring to the high-level structure of the block, rather than the particular implementation of its subcomponents. Some evidence for this hypothesis comes from [27], who used a simple isotropic purely convolutional model, called “ConvMixer,” that takes non-overlapping patch embeddings as inputs. Given an equal parameter budget, their model shows improved accuracy compared to standard ResNets and DeiT. A more thorough analysis of this hypothesis was performed by “A ConvNet for the 2020s,” [28], which systematically examined the impact of block elements 1-4, finding a purely convolutional model reaching SOTA performance on ImageNet, even when trained on IN-1K alone.
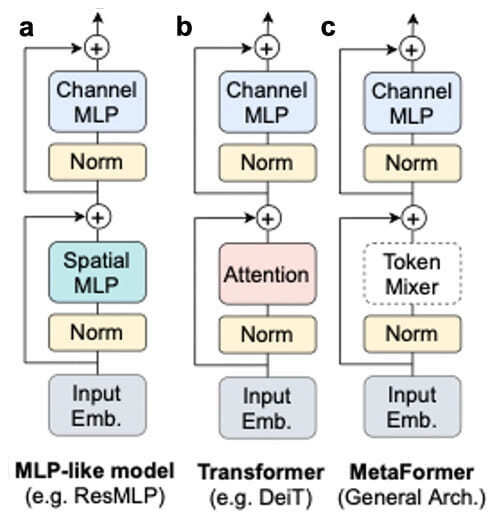
Figure 2. a. V-MLP, b. Transformer and c. MetaFormer. Adapted from [24].



